高中半角公式推导过程讲解

在高中数学中，我们经常接触到各种各样的公式。在这些公式中，有些是半角公式，它们在我们解题的过程中起着非常重要的作用。

那么，半角公式是什么？如何推导得出呢？接下来，我们就来详细地介绍一下高中半角公式的推导过程。

什么是半角公式？

在数学中，我们常常会遇到三角函数。三角函数中经常会用到不同角度的正弦、余弦、正切等函数值的比较。

在解决这些问题时，我们一般需要求出一个角度的正弦、余弦、正切值，然后再用它们进行计算。而半角公式就是用来求解半角的正弦、余弦、正切值的一些公式。

半角公式的推导过程

半角公式的推导过程实际上就是将一个任意角度的正弦、余弦、正切值表示成半角的正弦、余弦、正切值。首先，我们来推导正弦的半角公式。

正弦的半角公式

假设角A的大小为α，则有：

sin A = sin α

cos A = cos α

又：

sin α = 2sin(α/2)cos(α/2)

所以：

sin A = 2sin(A/2)cos(A/2)

其中，sin(A/2)可以表示成cos(π/4-A/2)或sin(π/4-A/2)之一，即：

sin(A/2) = cos(π/4-A/2) 或 sin(π/4-A/2)

当A

当A>π/2时，我们取sin(A/2) = cos(A/2-π/4)

因此，正弦的半角公式为：

sin(A/2) = ±sqrt[(1-cosA)/2]

其中，当A π时，取“-”号。

余弦的半角公式

同样地，我们可以得到余弦的半角公式：

cos(A/2) = ±sqrt[(1+cosA)/2]

当A π时，取“-”号。

正切的半角公式

最后，我们再来推导一下正切的半角公式。由于tanA=sinA/cosA，所以我们可以用正弦和余弦的半角公式来得到正切的半角公式。具体步骤如下：

tan(A/2) = sin(A/2)/cos(A/2) = 2sin(A/2)cos(A/2) / [cos^2(A/2) - sin^2(A/2)]

= (2/cosA) · sin(A/2) · cos(A/2) / [1 - sin^2(A/2)/cos^2(A/2)]

= (1+cosA)/[sinA]

因此，正切的半角公式为：

tan(A/2) = ±sqrt[(1-cosA)/(1+cosA)]

当A π时，取“-”号。

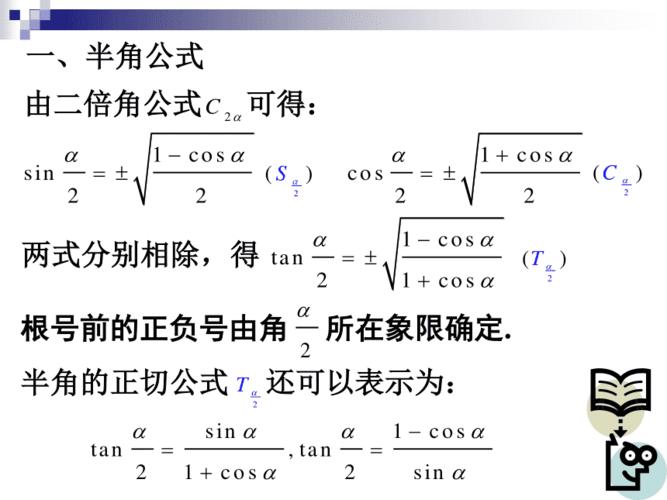
通过上面的推导过程，我们可以得到三角函数的半角公式。

在实际的解题过程中，半角公式能够帮助我们更加方便地求解各种三角函数值。因此，对于高中数学学习来说，掌握半角公式是非常重要的。