垂直平分线的定义判定和性质

垂直平分线是指平面内一条线段的中垂线，它将该线段垂直平分为两半。对于一个线段 AB，它的垂直平分线可以表示为 CD，CD 是 AB 的中垂线，即 CD 与 AB 垂直，并将 AB 平分为两个等长的线段 AC 和 BC。

垂直平分线的判定

判定一条线段的中垂线是否存在，可以使用尺规作图的方法。具体步骤如下：

步骤1：使用直尺将线段 AB 画成一条直线。

步骤2：以 A 点为圆心，以 AB 的长度为半径，画一个圆。

步骤3：以 B 点为圆心，以 AB 的长度为半径，画一个圆。

步骤4：两个圆相交的两个交点分别为 C 和 D。

步骤5：连接 CD，CD 就是线段 AB 的中垂线。

垂直平分线的性质

垂直平分线有如下性质：

（1）垂直平分线与线段的相交点是线段的中点。

即线段 AB 的中垂线 CD 与 AB 相交于点 E，则 AE=EB。

（2）垂直平分线同时垂直于线段 AB 的两侧。

即垂直平分线 CD 与线段 AB 的两边 AC 和 BC 垂直。

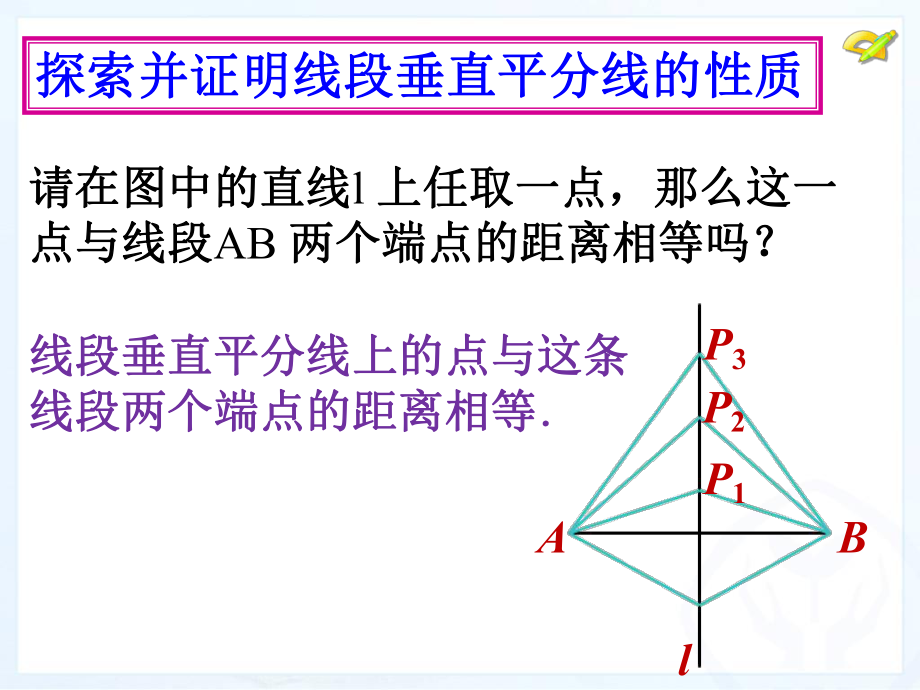
（3）如果从一个点 P 到线段 AB 的距离相等，那么这个点就在垂直平分线上。

即对于点 P 在平面上的任意位置，如果 AP=BP，则 P 在线段 AB 的中垂线 CD 上。

（4）如果垂直平分线与另一条线段相交，则两条线段相等。

即如果垂直平分线 CD 与另一条线段 EF 相交于点 G，则 CG=GD，即 EF=AB。

垂直平分线是几何学中非常重要的概念，它不仅具有理论上的意义，也有着广泛的应用。

在工程设计中，我们经常使用垂直平分线来确定物体的中心或者将物体平分为两半。

在数学竞赛中，垂直平分线也是一个重要的考点。因此，掌握垂直平分线的概念、判定和性质，对于学生来说是非常重要的。